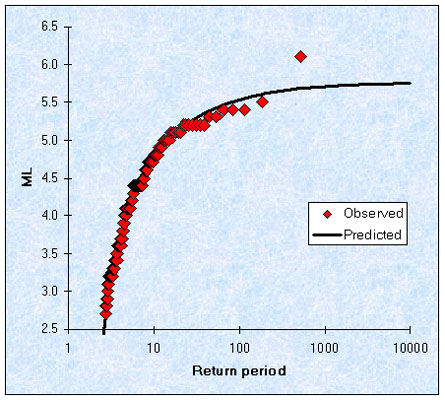
The statistical method
One step up from the observational method described above is to apply statistical methods to the observed earthquake record to calculate the probability of future events. This relies usually on the method of extreme values based on the work of the mathematician Gumbel. Simplified greatly, the theory states that if you know what was the extreme (i.e. highest observed) earthquake ground motion at your site each year (or every five years, or whatever), then by applying the statistical properties of distributions of extreme values, you can work out the probability of what the extreme value in the next fifty years will be, or even the limiting maximum value.
Seismologists have tended to be suspicious of this method on the grounds that it actually involves discarding most of your data, except for the extreme values. Can a method based on 5% of your data actually give better predictions than one based on 100%? Is there really such a thing as a free lunch? In practice, the main problem with this technique is that any calculations that go beyond the length of your input catalogue have very high uncertainties attached to them. (E.g. if your catalogue has 100 years of data, then you can use the method to calculate the once-in-100 year earthquake with reasonable confidence, but if you want the once-in-200 year event the error bars will be too big for the value to be really useful).